72-Edit Distance

100-Same Tree | Links:

题意

Given two words word1 and word2, find the minimum number of operations required to convert word1 to word2. You have the following 3 operations permitted on a word:

• Insert a character
• Delete a character
• Replace a character

Example 1:
Input: word1 = "horse", word2 = "ros"
Output: 3
Explanation: 
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')

Example 2:
Input: word1 = "intention", word2 = "execution"
Output: 5
Explanation: 
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')

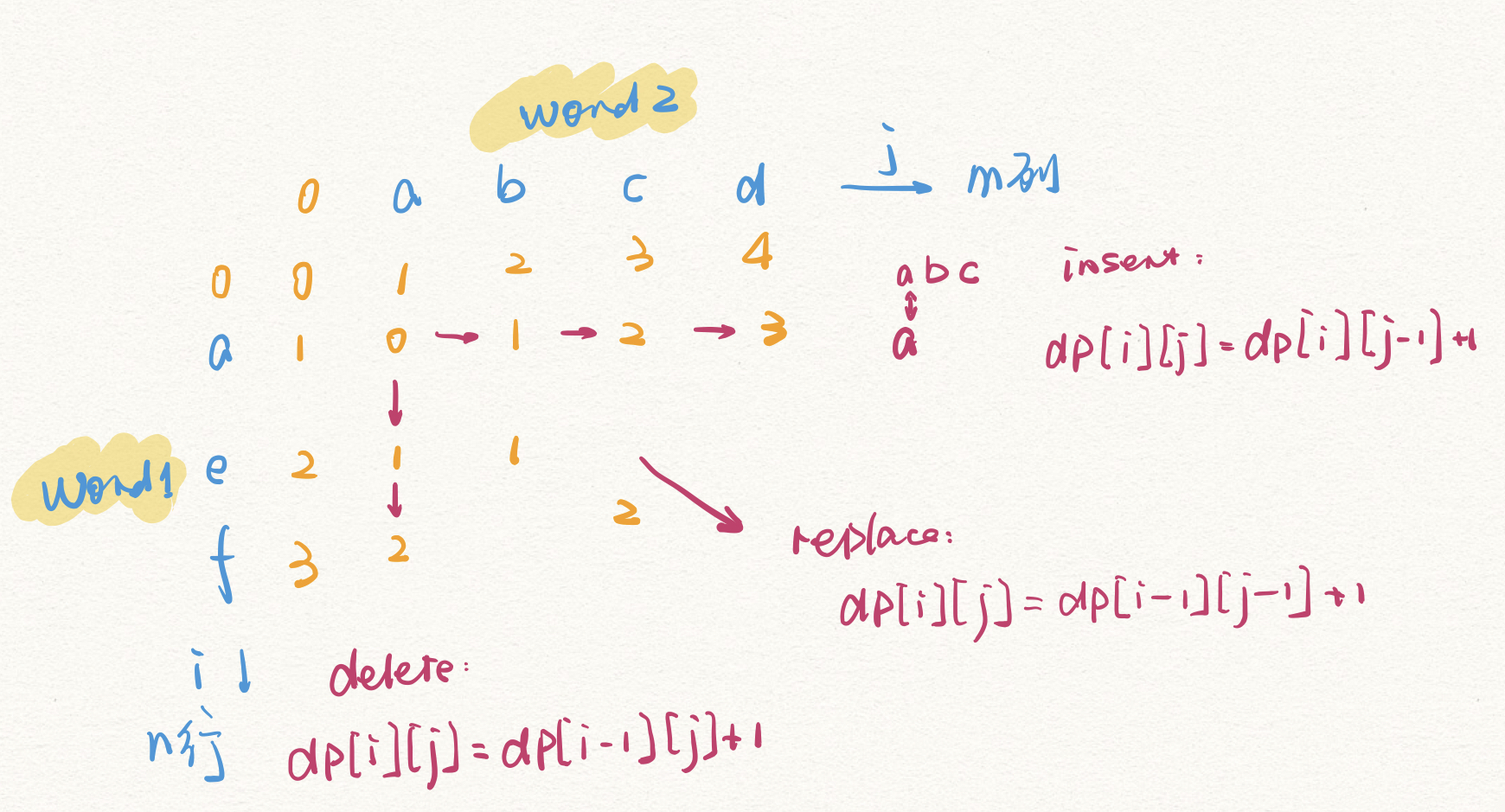
思路

• 动态规划
• dp[m][n]记录Word1前m-1个字符到word2前n-1个字符的edit distance
• 先初始化状态矩阵
• 再找状态转移函数

class Solution(object):
    def minDistance(self, word1, word2):
        """
        :type word1: str
        :type word2: str
        :rtype: int
        """
        m, n = len(word1), len(word2)
        dp = [[0 for _ in range(n+1)] for _ in range(m+1)]
        
        for i in range(m+1):
            dp[i][0] = i
        
        for j in range(n+1):
            dp[0][j] = j
            
        for i in range(1, m+1):
            for j in range(1, n+1):
                if word1[i-1] == word2[j-1]: # 当前位置字母相同-> 等同上一个状态
                    dp[i][j] = dp[i-1][j-1]
                if word1[i-1] != word2[j-1]: # 不同字母-> 增/删/改最小值 + 1
                    dp[i][j] = min(dp[i][j-1], dp[i-1][j], dp[i-1][j-1]) + 1
        return dp[m][n]