正则化

100-Same Tree | Links:

正则化用途

1. 对模型的复杂性进行惩罚，控制过拟合/高方差， 不让模型“无法无天”；
2. 限制参数搜索空间 ->在有约束的前提下逼近结果

L1正则化 Lasso

• 找到一条直线最好地去接近【拟合】所有样本点

• 损失函数 + $$\lambda \sum_{j=1}^{n}\left

  \theta_{j}\right

  $$ 参数绝对值之和

• 次要feature参数压缩为0 -> 得到一个简易模型， 易解释

L2正则化 Ridge

• 损失函数 + \(\lambda \sum_{j=1}^{n} \theta_{j}^{2}\) 参数平方和 -> 求导更容易
• 次要feature参数无限接近于0，不会等于0 -> 不会剔除变量，对方差控制更好

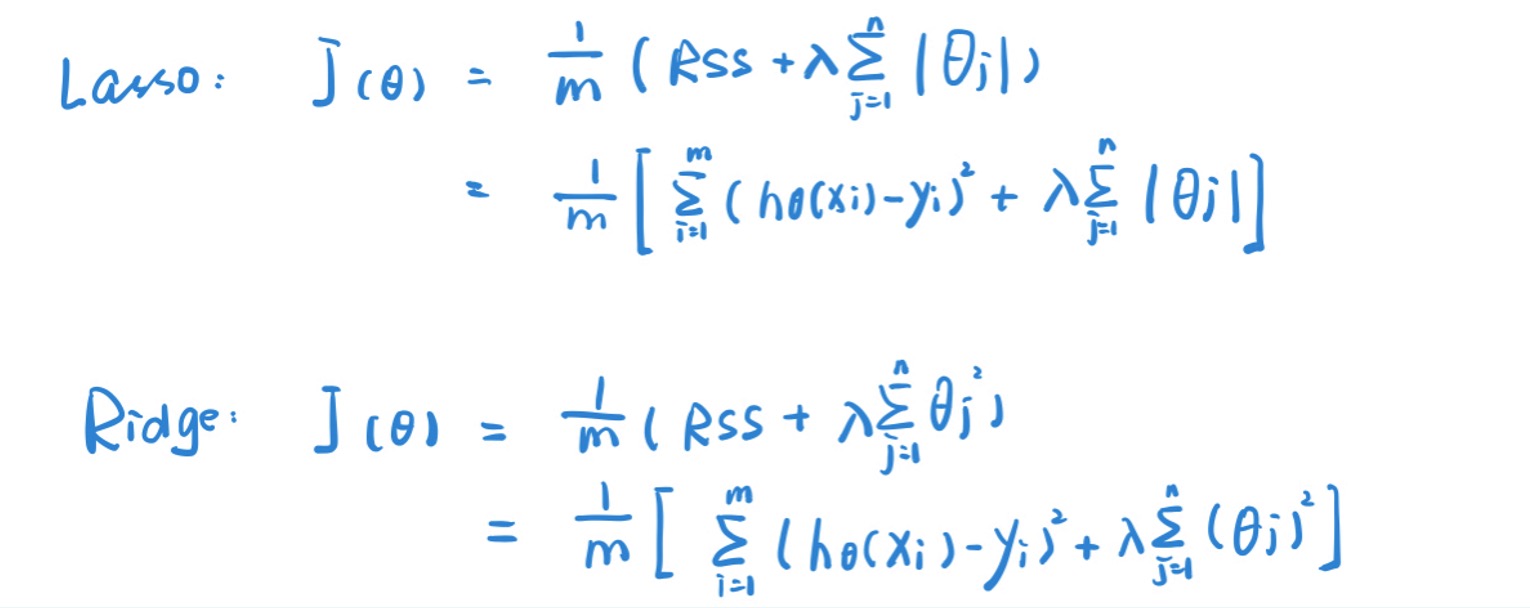
正则化关键

• 随着惩罚系数增加，通过小幅度增加偏差，实现方差大幅度下降
• 正则化之前要进行standardize/scale