逻辑回归

100-Same Tree | Links:

Overview

• Logistic Regression名字叫回归，实际是分类算法。将线性拟合结果通过一个激活函数【最常见sigmoid函数】映射为一个(0,1)的概率值，从而完成对事件发生概率的预测

• Logistic regression相当于单层神经网络
  
  
  

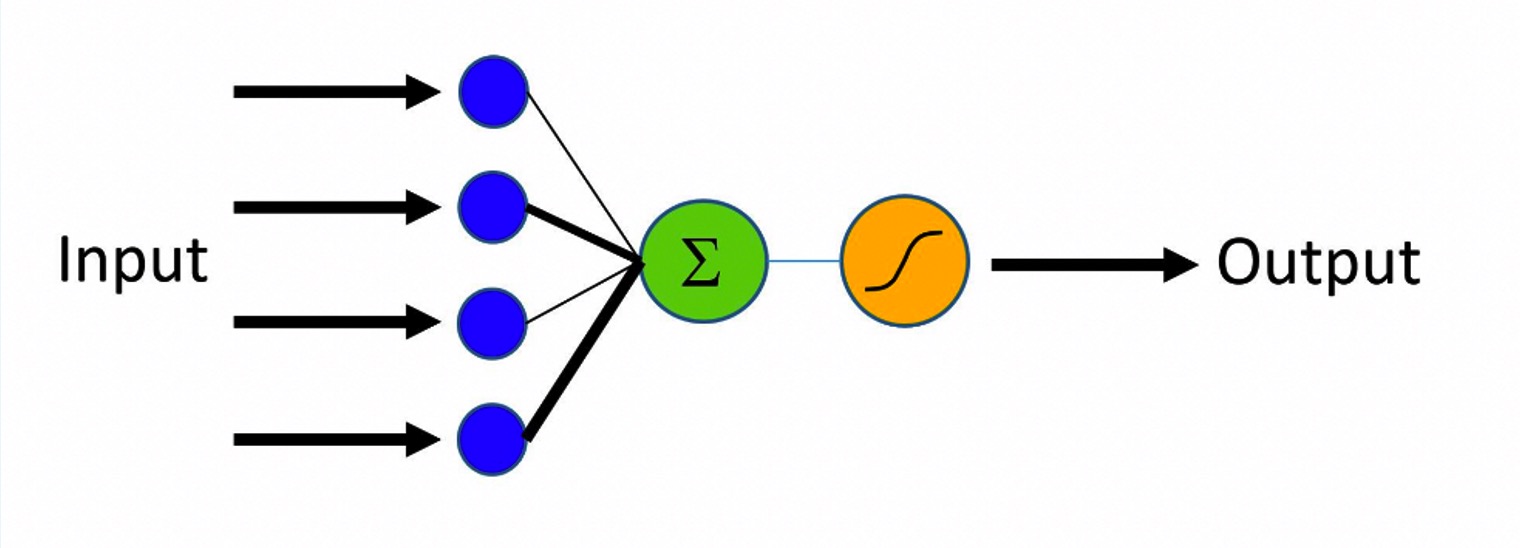
• 优
  • 擅长解决线性可分的问题， 其最终目标是确定决策边界
    • 容易解释,扩展性强,工程实现简单
• 劣
  • 特征工程量大【模型本身不能表达非线性关系，需要把特征做出来】,难以表达复杂组合关系

关键

• 逻辑回归的关键在于，将原本输出结果范围可以非常大的Xθ 通过sigmoid函数映射到(0,1)，从而完成概率的估测。
• 通常以0.5为界对概率进行分类
• 以AUC为metric可以找最佳分界点 ->Youden’s J-Statistic：最大化tpr-fpr
• 损失函数是凸函数，求解逻辑回归参数的方法是梯度下降，构造为凸函数的代价函数后，每次沿着偏导方向(下降速度最快方向)迈进一小部分，直至N次迭代后到达最低点。

模型优化方向

• 加入交互项 Interaction
• 加入非线性：polynomial feature
• 正则化 regularization: L1, L2, elastic net

应对多分类问题

• 本质上Logistic regression只能完成二分类
• 处理多分类思路有两种
  • one vs. one：每两个分类之间确定一个决策边界，取概率最大者作为自己的类别
  • one vs. rest：对于是此类/不是此类确定n个决策边界，取概率最大者作为自己的类别

Softmax

• softmax是Logistic Regression在多分类的推广，各个类别之间互斥
• softmax函数将原始概率分布进行e的指数次方变换并进行归一化，视作每个类别的概率 -> 使得所有类别的概率之和为1
• Softma使用交叉熵损失函数
  
  
  

多分类logistic regression vs. softmax

• 类别之间互斥用softmax
• 类别之间有相交用multinomial logistic regression