优化问题和基于梯度的方法

100-Same Tree | Links:

优化问题

  • 优化问题，从数学上来讲是最小化的问题，找局部极小值的问题
  • 两种基本优化方法
    • 无约束最小化问题
      1. 解析解方法：令导数等于0，求参数
        • 令导数/梯度等于0，可以找到函数的‘临界点’，在这个点处函数为极大值/极小值
        • 当目标函数是多元函数时，让目标函数的每一个偏导数为0，求参数
        • 劣：计算量大 / 有时不存在解析解
      2. 基于梯度的方法：常用
        • 梯度下降法/ 牛顿法：区别在于优化时使用了几阶导数/泰勒展开
    • 有约束条件的最小化问题： 拉格朗日乘子法

泰勒展开

  • 泰勒展开：用函数在某点上的取值来逼近附近取值，展开越多越接近 \(f(x)=\sum_{n=0}^{\infty} \frac{f^{(n)}\left(x_{0}\right)}{n !}\left(x-x_{0}\right)^{n}\)
    • 一阶泰勒展开： \(f(x) \approx f\left(x_{0}\right)+f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)\)
    • 二阶泰勒展开： \(f(x) \approx f\left(x_{0}\right)+f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)+f^{\prime \prime}\left(x_{0}\right) \frac{\left(x-x_{0}\right)^{2}}{2}\)
    • n阶泰勒展开： \(f(x)=f\left(x_{0}\right)+f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)+\frac{f^{\prime \prime}\left(x_{0}\right)}{2 !}\left(x-x_{0}\right)^{2}+\cdots+\frac{f^{(n)}\left(x_{0}\right)}{n !}\left(x-x_{0}\right)^{n}+R_{n}(x)\)
  • 泰勒展开在GBDT上的应用：参数迭代或模型迭代,用前一个参数值来推测下一个参数值的结果 \(\begin{aligned} &x^{t}=x^{t-1}+\Delta t \rightarrow f\left(x^{t}\right) \text { 在t-1出做泰勒展开 }\\ &\mathrm{f}\left(x^{t}\right) \approx \mathrm{f}\left(x^{t-1}\right)+\mathrm{f}^{\prime}\left(x^{t-1}\right) \Delta x\\ &f\left(x^{t}\right) \approx f\left(x^{t-1}\right)+f^{\prime}\left(x^{t-1}\right) \Delta x+f^{\prime \prime}\left(x^{t-1}\right) \frac{\Delta x^{2}}{2} \end{aligned}\)

梯度下降法

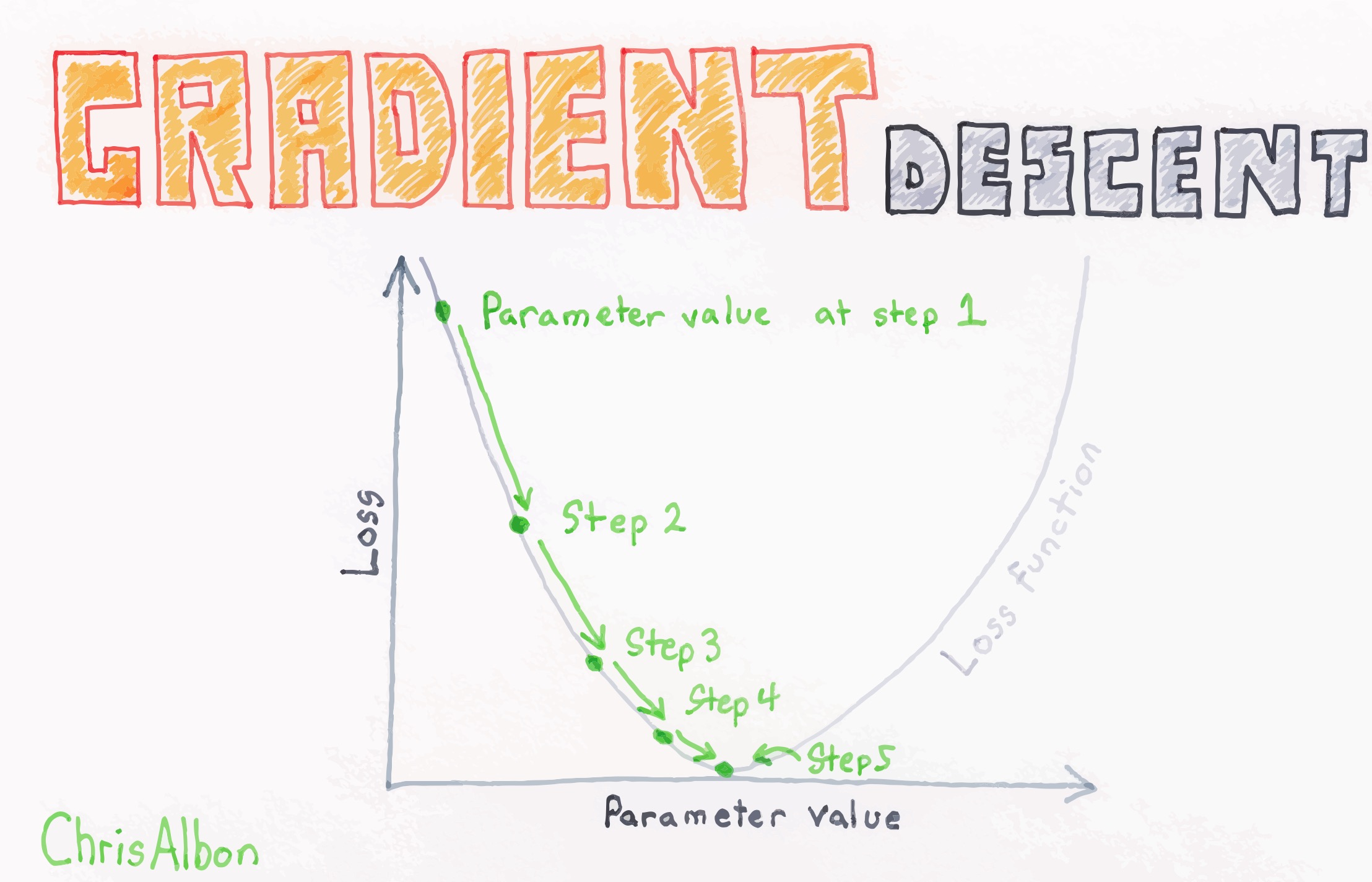
  • 机器学习的基本任务是最小化损失函数L(θ),其中θ是要求解的模型参数，可用梯度下降法求解
  • 梯度下降的本质
    • 选取初值\(\theta^{0}\)
    • 沿着负梯度的方向不断迭代-> 不断修正初始参数θ的值
    • 直至走到损失函数的最低点(极小化)


  • 如何求解下一个参数：梯度下降法用到一阶导 ->对损失函数进行一阶泰勒展开，α即步长 \(\begin{aligned} &\begin{array}{l} \theta^{t}=\theta^{t-1}+\Delta \theta \\ \mathrm{L}\left(\theta^{t}\right)=L\left(\theta^{t-1}+\Delta \theta\right) \approx L\left(\theta^{t-1}\right)+L^{\prime}\left(\theta^{t-1}\right)(\Delta \theta) \end{array}\\ &\text { 可将 } \Delta \theta \text { 常数化为 }-\alpha \mathrm{L}^{\prime}\left(\theta^{\mathrm{t}-1}\right) \text { 使得损失函数一定变小 }\\ &\rightarrow \theta^{t}=\theta^{t-1}-\alpha L^{\prime}\left(\theta^{t-1}\right) \end{aligned}\)

  • 注意：梯度下降找到的是局部极小值，不是全局极小值，但是已经足够好
  • 三种实现方式
    • Batch 批量梯度下降：梯度下降法最原始的形式，对全部的训练数据求得误差后再对θ进行更新
      • 优劣：每步都趋向全局最优解；每次迭代用到所有训练样本，计算量大，训练速度慢
    • SGD随机梯度下降：每次迭代使用一个训练样本计算梯度，在一个epoch中遍历完所有训练样本
      • 优劣：提升训练速度，但噪音比较多，并不是每次迭代都向着整体最优化方向
    • Mini Batch梯度下降：每次选取小批量（batch个）样本计算梯度
      • 优劣：训练过程比较快，也能参数训练的准确率
  • 应用：GBDT（Gradient Boosted Decision Tree） 在函数空间中利用梯度下降法进行优化

牛顿法

  • 对损失函数进行二阶泰勒展开，同时用到一阶导和二阶导 \(\begin{aligned} &L\left(\theta^{t}\right)=L\left(\theta^{t-1}+\Delta \theta\right) \approx L\left(\theta^{t-1}\right)+L^{\prime\left(\theta^{t-1}\right)}(\Delta \theta)+L^{\prime \prime}\left(\theta^{t-1}\right) \frac{\Delta \theta^{2}}{2}\\ &\text { 将一阶导, 二阶导记为g, } \mathrm{h}->\mathrm{L}\left(\theta^{t}\right) \approx L\left(\theta^{t-1}\right)+g(\Delta \theta)+h \frac{\Delta \theta^{2}}{2}\\ &\text{令} \Delta \theta=-\frac{g}{h} \text { 可让损失函数变小 }\\ &\rightarrow \theta^{t}=\theta^{t-1}-\frac{g}{h} \end{aligned}\)
  • 应用：XGBoost在函数空间中利用牛顿法进行优化，优化的方向是一阶导/二阶导的负方向

© 2020. All rights reserved.