置信区间与置信水平

100-Same Tree | Links:

Overview

• 置信区间，简单来说就是误差范围，用来描述某个数据估计准确程度 e.g. 如果用一定量的样本数据估计出APP用户的平均年龄为28岁，如果你收集了另外一组样本，其平均年龄为35岁。是否能判断前面的估计是错误的呢？
  
  
  

目标

• 根据中心极限定理，样本均值围绕在总体均值周围呈现正态分布。因此我们可以样本均值来估计总体均值
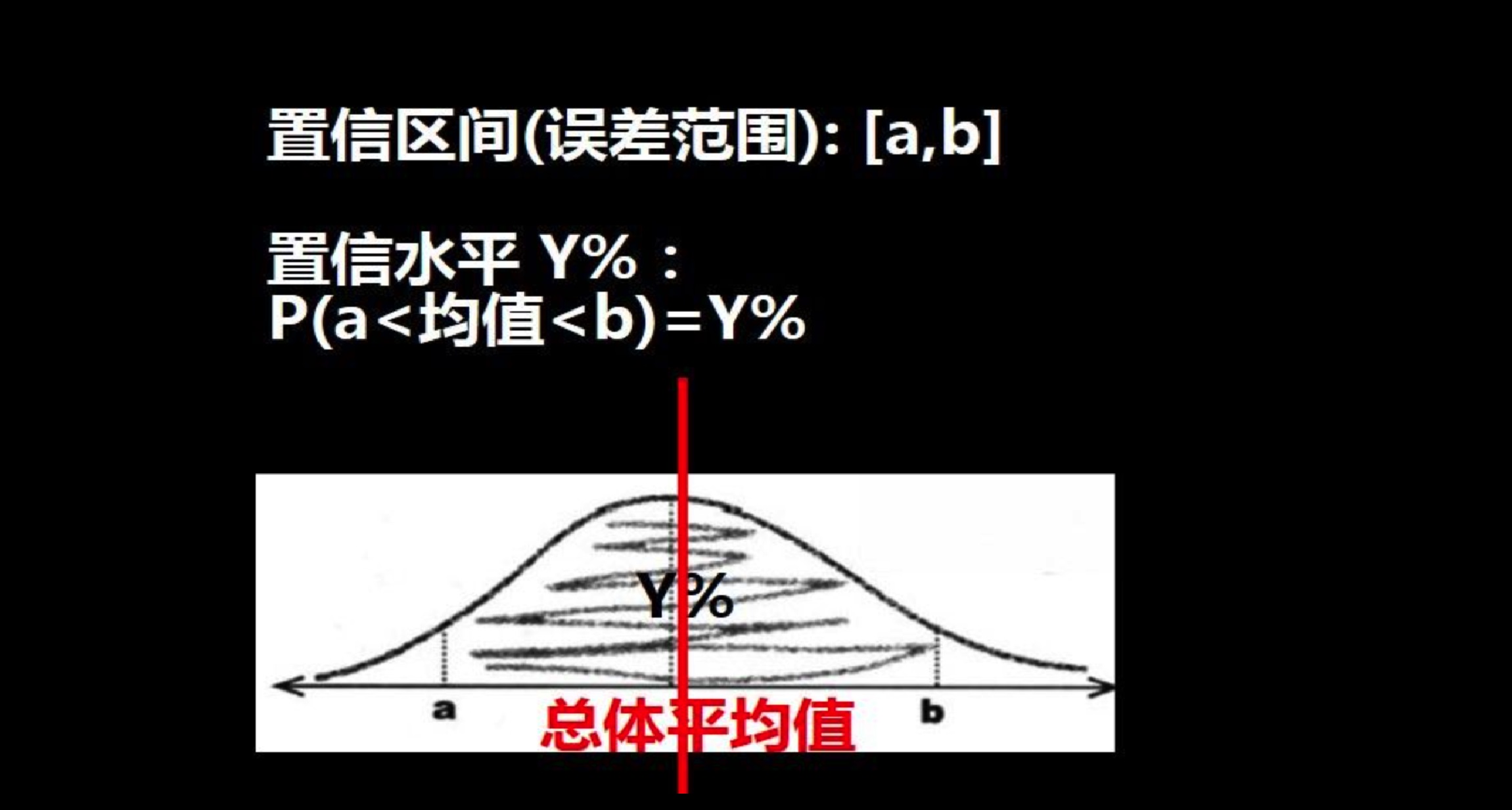
• 置信区间表示这种的误差范围的区间
• 置信区间取决于置信水平：“置信区间中包含总体均值”这一结果具有的可信程度/概率
  • 常用置信水平是95%，对应着两个标准误差范围内
  • 95%置信水平的涵义：如果我100次抽样，会有95次在这个置信区间包含了总体平均值
  • 置信水平越高，置信区间越宽，置信区间包含总体均值的概率越大

如何计算置信区间

1. 确定问题：药物A对神经的反应时间
   • 需要为总体均值构建一个置信区间
   • 需要抽取一个合适的样本集，通过样本数据估计总体数据
2. 求样本均值和标准误差
   • 当样本大于30时，抽取的样本符合中心极限定理
   • 抽样实验：找来100只老鼠作为样本来做实验，对每只老鼠注射药物A，对其机型神经刺激，并记录反映时间
   • 计算样本平均值是1.05秒，样本标准差是0.5
   • 计算标准误差
     \(SE= \frac{s样本标准差}{\sqrt{n样本大小}} = \frac{0.5}{\sqrt{100} } =0.05秒\)
3. 确定置信水平α
   • 常用置信水平95%
4. 计算置信区间
   • 置信区间：\([总体均值-zscore*SE, 总体均值+zscore*SE]\)
   • 根据(1−α)/2 查表可得z-score
     
     
     
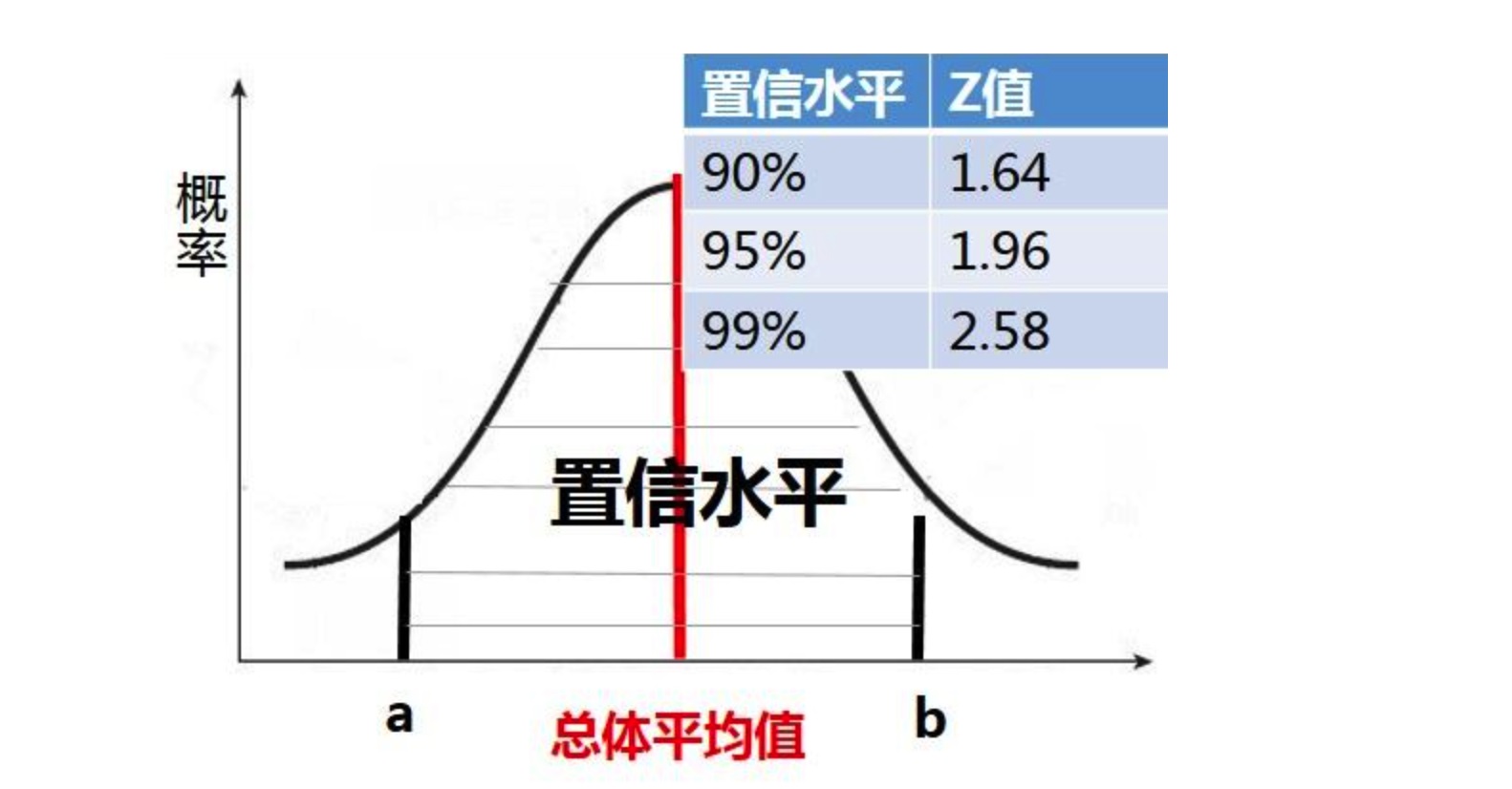
   • 实验结果 \(a = 总体均值-zscore*SE = 1.05-1.96*0.05=-0.952\) \(b = 总体均值+zscore*SE = 1.05+1.96*0.05=1.148\) \(置信水平95% 置信区间[-0.952,1.148]\)