中心极限定理

100-Same Tree | Links:

用途

• 用途1：没有总体信息情况下，可以用样本估计总体
• 用途2：判断某个样本是否属于总体(3个标准差以内)

用样本平均值估计总体平均值

• 中心极限定理：样本平均值约等于总体均值
• 不管总体是什么分布，样本均值围绕在总体均值周围呈现正态分布
• 样本大小必须达到30，中心极限定理才能保证成立。
• 取样次数越多，结果就越接近正态分布；而且样本大小越大，分布就越接近正态分布。

用样本标准差估计总体标准差

• 由于样本的标准差要小于总体标准差，因此分母变更为n-1
• 样本标准差衡量数据集的波动大小
  \(\text {数据样本的标准差} =\sqrt{\frac{\sum(x-\mu)^{2}}{n}}\)
  \(\text {估计总体的标准差}=\sqrt{\frac{\sum(x-\mu)^{2}}{n-1}}\)

标准误差

• 标准误差是所有样本集平均值的标准差
• 标准误差是用来衡量样本平均值的波动大小
  
  
  
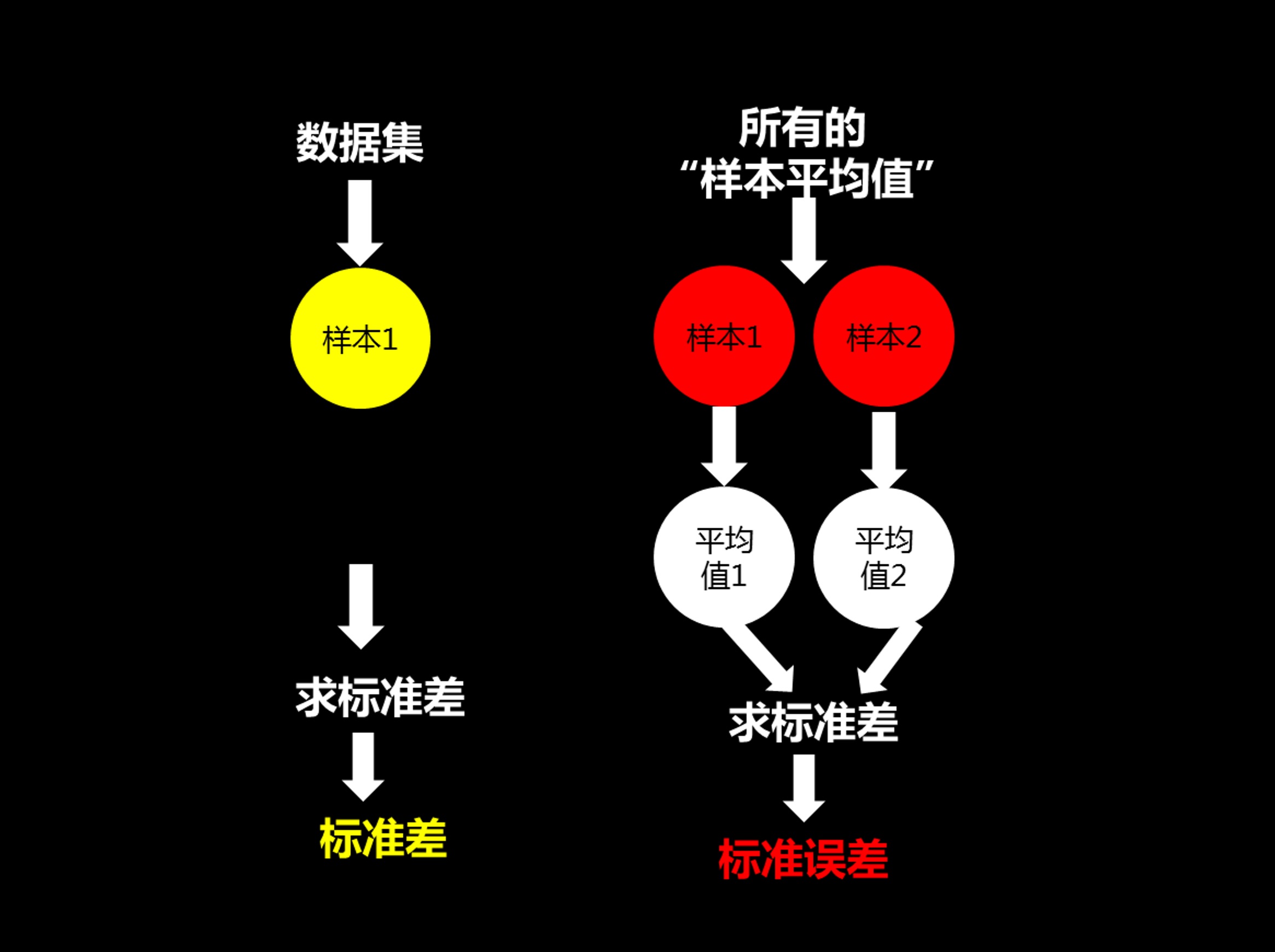
• 通过总体标准差估算标准误差 \(\mathrm{SE}=\frac{s \text { 总体标准差 }}{\sqrt{n}}\)

样本平均值概率分布

• 样本平均值概率
  
  
  
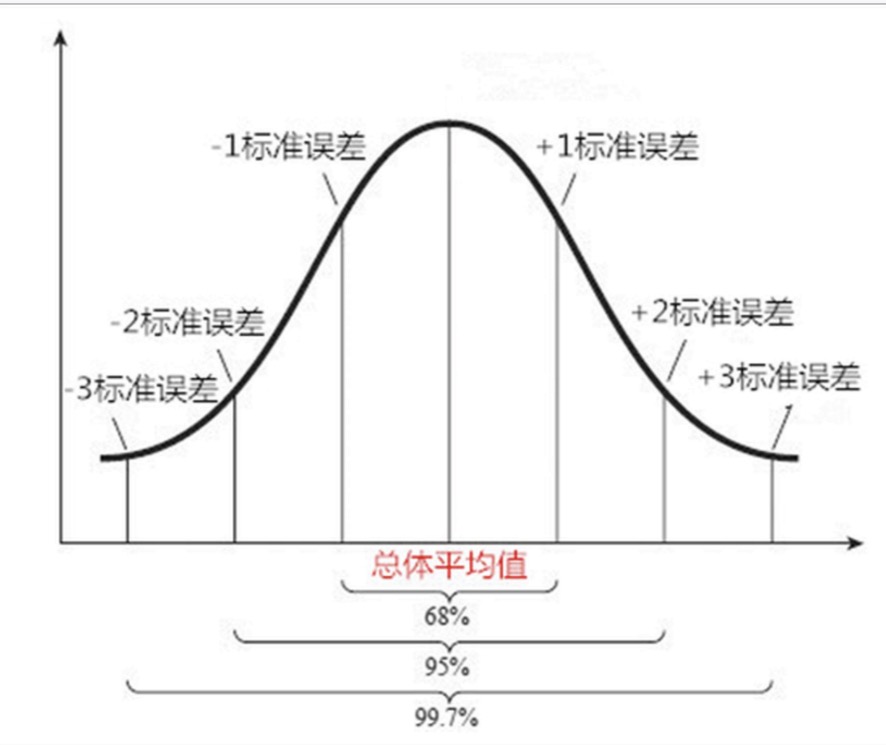
• 判断样本是否属于总体
  • 有68%的样本平均值会在总体平均值一个标准误差的范围之内
  • 有95%的样本平均值会在总体平均值的两个标准误差的范围之内
  • 有99.7%的样本平均值会在总体平均值3个标准误差的范围之内。
• 如何使用：假如某个样本的平均值减去总体的平均值，大于3个标准误差 -> 可判断该样本不属于总体