SVM支持向量机
100-Same Tree | Links:
Overview
- 支持向量机是一种监督学习算法,它学习的目标是在特征空间中找到能将不同组点去开来的,间隔margin最大化的超平面
- 在中小型数据集表现好,在大数据集跑不动
- 不同于perceptron希望所有点远离超平面, SVM只关注最有价值的那些样本点【supporting vector】
- SVM 既支持二元分类也支持多元分类
- 可支持分类问题,也支持回归问题
SVM的内核
- 最大间隔分类器maximum margin classifier
三种SVM形式
- 硬间隔支持向量机Hard Margin:不允许出现任何点出现在间隔内,应对线性可分问题
- 软间隔支持向量机 Soft Margin:允许出现分类错误的点或点可以进入margin,应对近似线性可分问题
- 非线性支持向量机 Kernel-based:使用核函数和软间隔最大化,解决非线性问题
几个核心概念
- 超平面:在n维空间中总会有一个n-1空间将点分开 e.g. 在一维空间中是一个点,二维空间中是一条线,高维空间中是一个超平面
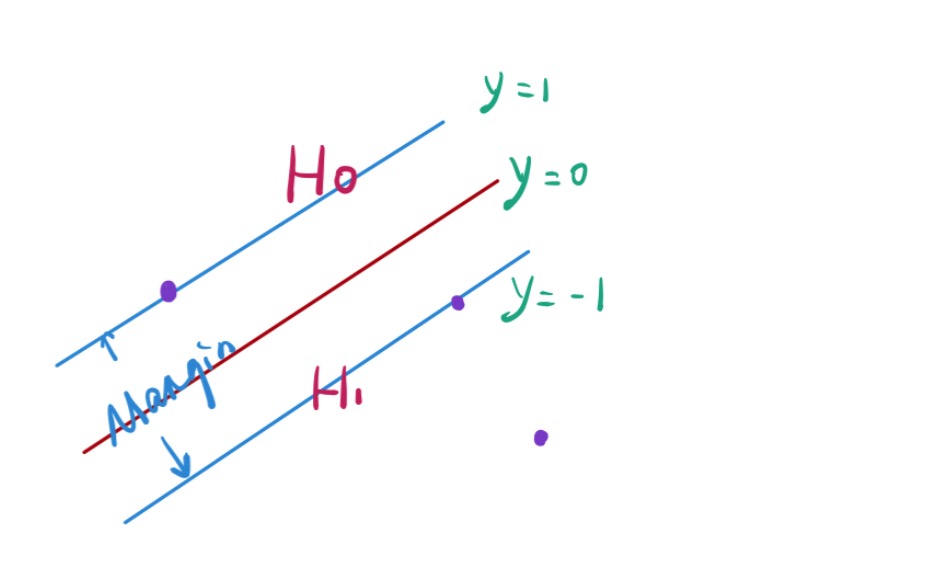
- 最优分离超平面 maximum margin classifier: 最大程度地将不同组地点分开,尽可能远离所有类别的点【margin最大】,即我们要找的决策面【超平面】
- 支持向量:两组数据中与超平面最近的点
- 间隔margin:支持向量与超平面之间的距离
- 学习目标:最优分离超平面要求远离所有点,即最大化margin
- 决策边界只跟支持向量有关系,跟其它点没有关系
- SVM 通过间隔最大化可以将优化问题转换成一个凸优化问题,这时解是唯一的。
假设函数
\(\begin{aligned} \hat{y}=\operatorname{sign}\left(w^{T} x+b\right) \\ \text { 其中 } \operatorname{sign}(x)=\left\{\begin{array}{ll} -1 & x<0 \\ 1 & x \geq 0 \end{array}\right. \end{aligned}\)
损失函数
-
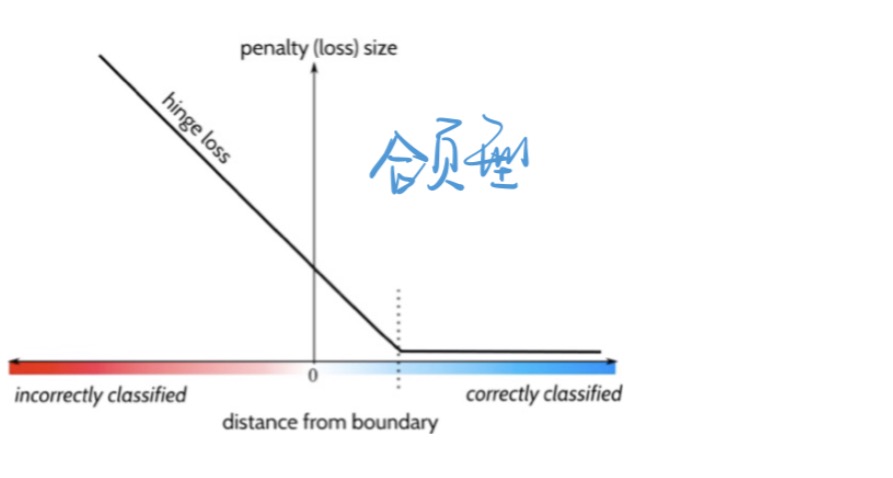
Hinge Loss(合页形): \(J(z)=\max (0,1-z)\)
-
SVM的损失函数:\(J(\theta)=\max \{0,1-y \hat{y}\}\)
- 如果点被正确分类,且在支持向量以外,损失是 0
- 如果点被正确分类,且在margin之内,损失为小于1的小数
- 如果点被分类错误,损失函数大于1,且随样本到超平面距离的增大,损失函数增大。
优化问题
- hyperplane \(=w^{T} x+b\)
- 点到平面的几何距离 \(=\frac{y\left(w^{T} x+b\right)}{\|w\|_{2}}\)
- margin \(=\frac{2}{\|w\|_{2}}\)
- 优化问题 \(\max \frac{2}{\|w\|_{2}}\) subject to \(y_{i}\left(w^{T} x+b\right) \geq 1(i=12, \ldots m)\)
- 优化目标:最大化Margin,同时保证其他样本点在H1和H2 (支持向量)以外
- 优化问题转化为:在所有满足约束条件的超平面中, 选择具有最小 \(\|\mathbf{w}\|\) 的超平面,这意味着最大间隔
- 如何求解:一个带约束的凸二次规划问题 -> 用拉格朗日乘子法 + 对偶问题的思路来求解
- 最终推导:支持向量分类器的优化问题的解-> 只涉及点的内积 inner product, 不涉及点本身 \(\begin{aligned} f(x) &=\left(\sum_{i=1}^{n} \alpha_{i} y_{i} x_{i}\right)^{T} x+b \\ &=\sum_{i=1}^{n} \alpha_{i} y_{i}\left\langle x_{i}, x\right\rangle+b \end{aligned}\)
软间隔支持向量机
- 允许某一些数据点不满足约束:允许一些点落间隔错误的一侧,甚至超平面错误的一侧
- 寻找一个超平面:将大部分的训练观测正确区分开来
- 引入松弛变量:1- ε表示样本点到决策超平面之间的距离,允许这个距离小于1
- 引入参数C:对错分的点进行惩罚
- C= 0 : 相当于硬间隔,不允许存在穿过间隔的观测
- C>0: 允许不超过C个点可以落在超平面错误的一侧
- C越大,说明分错的代价太大,分类器会竭尽全力分对所有点-> 可能造成过拟合
核函数
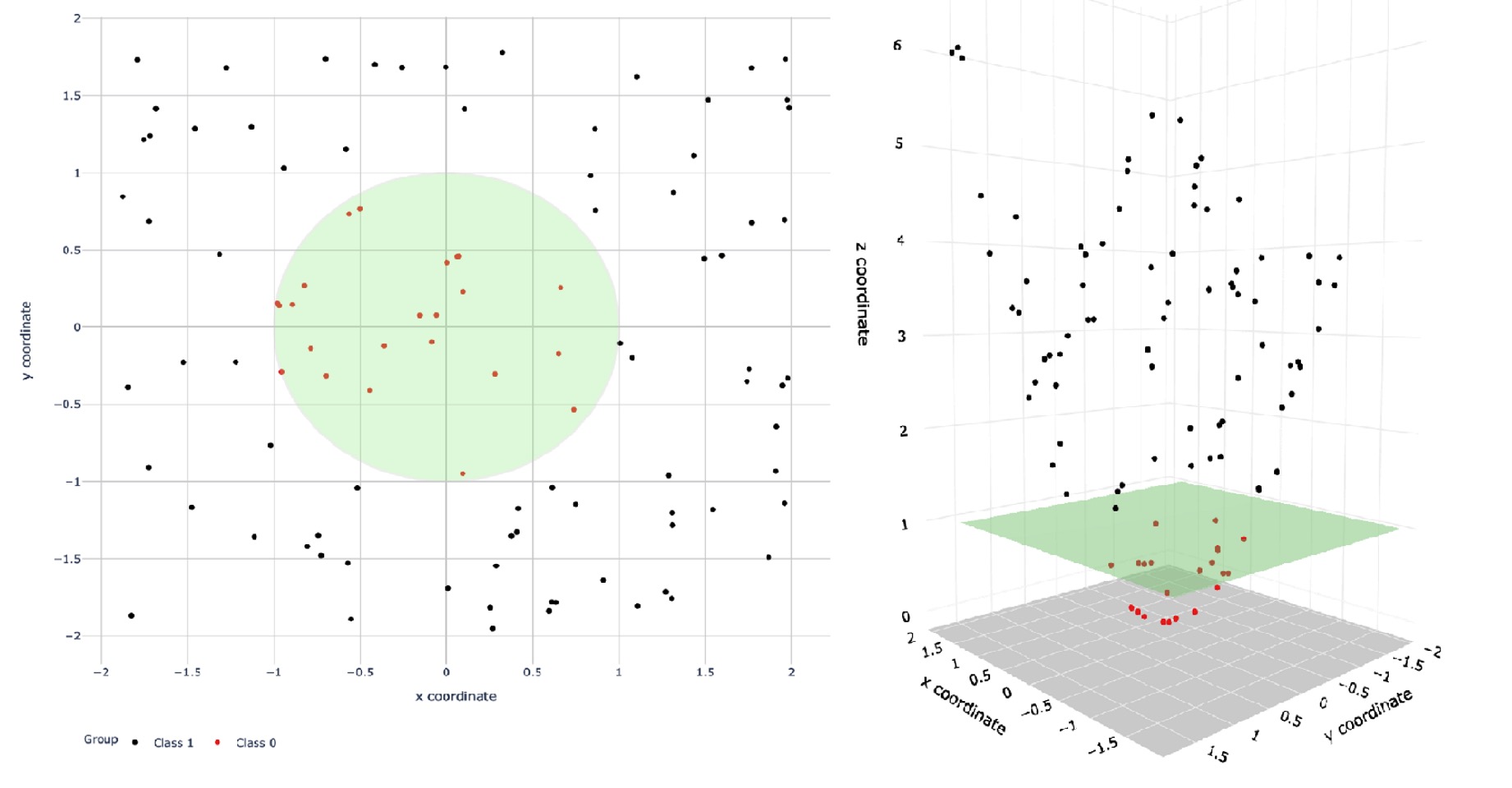
- 面对线性不可分的问题,引入核函数
-
使用核函数kernel来扩大特征空间,将低维原始空间映射到高维特征空间,使得数据集在高维空间中变得线性可分,从而再使用线性学习器分类。
- 核函数的定义为特征空间的内积: \(\mathrm{K}(\mathrm{x}, \mathrm{y})=<\mathrm{x}, \mathrm{y}>=\phi(x)^{T} \phi(y)\)
- 因为支持向量分类器的优化问题的解-> 只涉及点的内积->可定义核函数来代替内积
- 因为支持向量分类器的优化问题的解-> 只涉及点的内积->可定义核函数来代替内积
几种核函数
- 线性核函数(Linear Kernel):\(K(x, y)=(x \cdot y)\)
- 主要用于线性可分以及样本数与特征数差不多的情况。
- 参数少,速度快
- 多项式核函数(Polynomial Kernel):\(\mathrm{K}(\mathrm{x}, \mathrm{y})=(\gamma \mathrm{x} \cdot y+r)^{p}\)
- 解决线性不可分问题,生成平滑决策边界
- γ, r,p 都需要调参
- 相当于将原始空间映射到p 维空间
- 高斯核函数(Gaussian Kernel/Radial Basis Function): \(\mathrm{K}(\mathrm{x}, \mathrm{y})=e^{-\gamma \||x-y|^{2}}\)
- 非线性分类SVM最主流的核函数。
- 参数 \(\gamma\) 需要调参
- 根据泰勒展开 \(e^{x} \approx 1+x+\frac{x^{2}}{2 !}+\frac{x^{3}}{3 !}+\ldots \frac{x^{n}}{n !}\) 可得到一个无穷维度的映射, 因此高斯核函数将原始空间映射到无穷维空间
- 参数gamma表示受数据集中哪些点的影响
- 小gamma: 考虑所有点,不容易捕捉超平面的形状-> get a smoothier surface
- 大Gamma:只考虑超平面附近的点,容易捕捉数据集的整体形状 -> get a spiky surface
SVM用于多分类
- One v.s. One:每两个类之间建一个SVM
- One v.s. rest:在每一类与其它k-1类之间建一个SVM