朴素贝叶斯
100-Same Tree | Links:
贝叶斯公式
- 条件B发生下事件A的条件概率: \(\mathbf{p}(\mathbf{A} \mid \mathbf{B})=\frac{P(A B)}{P(B)}\)
-
已知p(A|B), 求p(B|A) \(P(B \mid A)=\frac{P(A \mid B) P(B)}{P(A)}\)
- 贝叶斯最大的用途是打通了条件概率之间的通路 \(P(A \mid B)<->P(B \mid A)\)
朴素贝叶斯
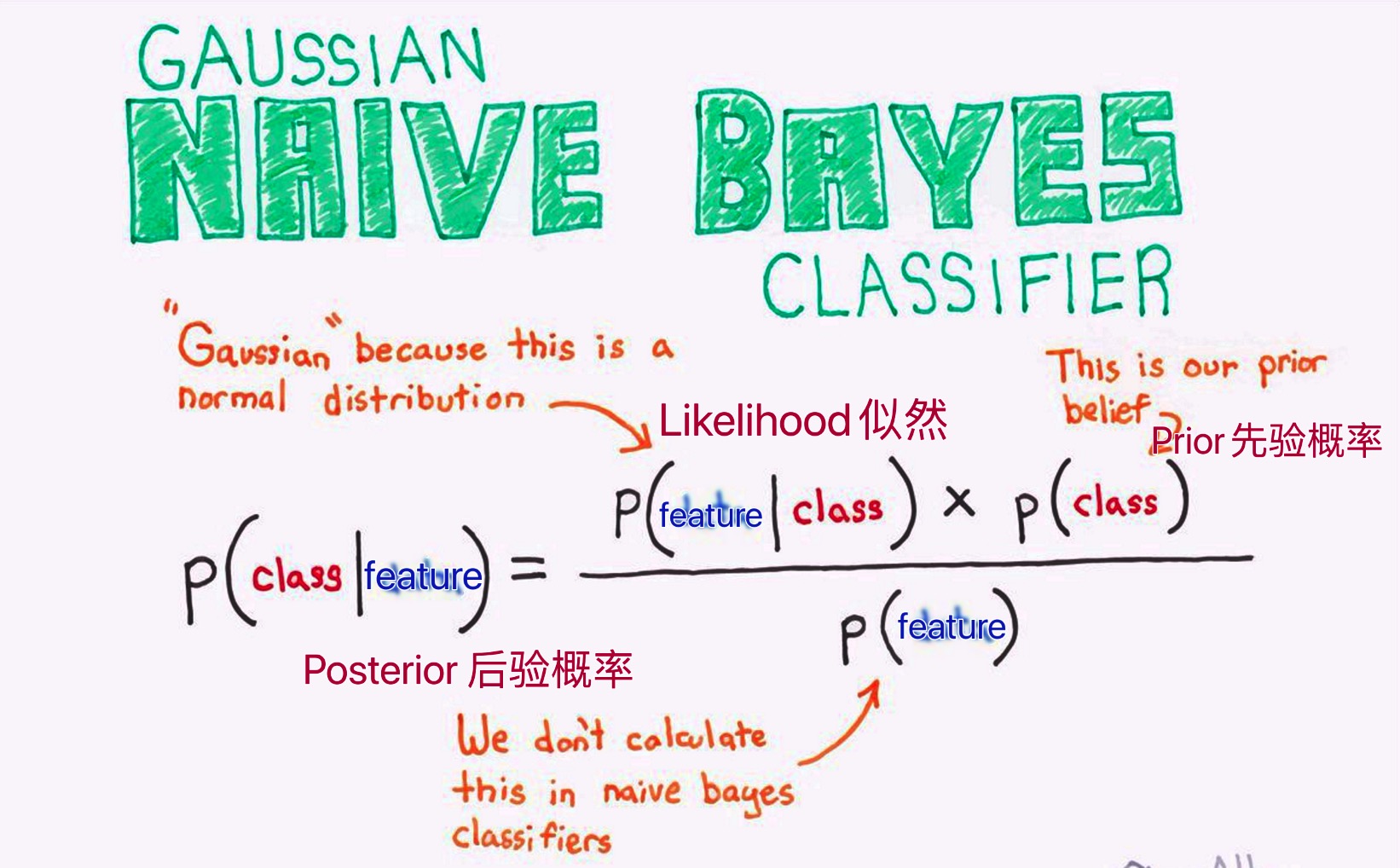
- 朴素贝叶斯:已知类别中特征的分布,求具有某些特征属于什么类别 \(P\left(y_{i} \mid x\right)=\frac{P\left(x \mid y_{i}\right) P\left(y_{i}\right)}{P(x)}\)
- 朴素贝叶斯 = 贝叶斯定理 + 条件独立假设 + 平滑(拉普拉斯平滑)
- 假设1:条件独立假设
- 某一特征的出现于其它特征无关 <-【“朴素”说法的来源,蠢萌】
- 某一个类别中的特征分布可以通过条件概率连乘获得 \(p\left(x \mid y_{i}\right)=p\left(a_{1} \mid y_{i}\right) p\left(a_{2} \mid y_{i}\right) \ldots p\left(a_{m} \mid y_{i}\right)=\prod_{j=1}^{m} p\left(a_{j} \mid y_{i}\right)\)
- 假设2:连续值特征属性服从正态分布
- 如果特征属性是连续值:计算出训练样本中各个类别中此特征的均值和标准差,代入高斯分布公式可得条件概率 \(g(x, \eta, \sigma)=\frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{(x-\eta)^{2}}{2 \sigma^{2}}}\) \(P\left(a_{k} \mid y_{i}\right)=g\left(a_{k}, \eta_{y_{i}}, \sigma_{y_{i}}\right)\)
- LapLace校准:为避免某些类别中某个特征为0 \(P(a \mid y)=0\) ->每个类别中每个特征计数 + 1
朴素贝叶斯流程
- 确定类别数量m和特征数量n
- m个特征\(\left\{\mathrm{a}_{1},\mathrm{a}_{2}, \ldots, \mathrm{a}_{\mathrm{m}}\right\} ;\) n个类别 \(\left\{\mathrm{y}_{1}, \mathrm{y}_{2}, \ldots, \mathrm{y}_{n}\right\}\)
- 建立分类器
- 统计各个类别出现的先验概率 \(P\left(y_{i}\right)\)
- 统计每个特征相对于每个类别的条件概率 \(\mathrm{P}\left(\mathrm{a}_{\mathrm{i}} \mid \mathrm{y}_{\mathrm{i}}\right)\)
- 推断后验概率 \(P\left(x \mid y_{i}\right) P\left(y_{i}\right)=P\left(a_{1} \mid y_{i}\right) P\left(a_{2} \mid y_{i}\right) \ldots P\left(a_{m} \mid y_{i}\right) P\left(y_{i}\right)\)
- 预估结果取 \(P\left(x \mid y_{i}\right) P\left(y_{i}\right)\) 最大项的类别