决策树
100-Same Tree | Links:
Overview
- 决策树既可用于分类模型,也可用于回归模型,常用来解决分类问题
- 决策树是非参数模型,树结构就是假设函数
- 优
- 逻辑清晰,可解释性好
- 树方便可视化
- 方便处理类别变量,不需要one-hot encoding
- 劣
- 贪婪算法:只考虑当前最优,可能找的不是最好的树
- 不够健壮:数据小幅度变化可能导致树的大幅变化
- 单个树方差高
决策树核心思想
- 【分而治之】:从根节点到叶进行递归,在每一个节点依据一个属性,不断地把树分为两支。算法关键在于选择最优划分属性。
- Top-down:从上到下,从根到叶
- 结果分为中间结点和叶结点,其中每个结点表示一个特征,叶结点代表一个类别
- Greedy: 着眼于当前最优,寻找最优划分属性
- Recursive:不断地把数据分成两组
- 如果数据点被完美划分:收工;否则,继续分治
- 三种停止条件
- 当前结点的所有数据属于同一类别:无需划分,作为叶子结点
- 当前数据特征相同:无法划分-> 判断为多数类别
- 当前结点的数据集为空:不能划分-> 划分为父节点中的多数类别
选择最优属性的指标
- 信息熵 entropy
- 衡量信息的不确定性/纯洁度
\(\operatorname{Ent}(\mathrm{D})=-\sum_{k=1}^{|y|} p_{k} \log p_{k}\) - 目标:越小越好(接近0);属性的信息熵越小越纯洁
- 衡量信息的不确定性/纯洁度
- 信息增益 Information Gain
- 计算信息熵下降了多少【ID3算法使用】
- 使用某个属性划分前的信息熵-划分后的信息熵,并使用各分支样本占比作为权重 \(\operatorname{Gain}(\mathbf{D}, \mathbf{A})=\operatorname{Ent}(\mathbf{D})-\sum_{v=1}^{V} \frac{\left|D^{v}\right|}{|D|} \operatorname{Ent}\left(D^{v}\right)\)
- 目标:越大越好;ID3寻找信息增益最大的属性,最大程度降低信息的不确定性
- 不良偏好:倾向取值数目多的属性 e.g. 用学号划分学生
- 信息增益率 Gain Ratio
- 【C4.5使用】对取值数目做惩罚,避免ID3的不良偏好
- 信息增益/ 样本离散程度 GainRatio(D,a) \(=\frac{\operatorname{Gain}(D, a)}{I V(a)}\) 其中, \(I V(a)=-\sum_{v-1}^{V} \frac{\left|D^{v}\right|}{|D|} \log _{2} \frac{\left|D^{v}\right|}{|D|}\) 某属性划分之后样本占比: 属性a的可能取值数目越多
- 目标:越大越好,C4.5算法在信息增益高于平均的情况下,优先找信息增益率高的属性
- 基尼指数 Gini Index
- 衡量信息的不确定性【CART使用】
- 从D中随机抽取两个样本,类别不一致的概率 \(\operatorname{Gini}(\mathrm{D})=1-\sum_{k=1}^{|y|} p_{k}^{2}\)
- 属性a的基尼指数 = 基尼指数*样本占比 Gini lndex GiniIndex \((\mathrm{D}, \mathrm{a})=\frac{\left|\mathrm{D}^{v}\right|}{\nu} \operatorname{Gini}\left(D^{v}\right)\)
- 目标:基本等价于Entropy越小越好, CART寻找Gini Index最小的属性,Gini Index越小越纯洁
连续值与缺失值
- 连续值:把一个连续属性按取值划分为相应的bin e.g. 两个值0.3, 0.5,划分为<0.4与>=0.4
- 缺失值
- 某个属性中出现缺失值,使用未缺失的部分判断划分属性的优劣
- 缺失值同时进入所有分支,根据样本占比赋予权重
- e.g 某个属性分为1/5大,1/5中,3/5小,两个样本在这个属性上缺失,则按1/5,1/5,3/5的比例进入三个分支,参与指标的计算
剪枝
- 分类决策树避免过拟合的方式:剪枝
- 两种剪枝策略
- 预剪枝:每次特征划分的时候,先在验证集上做预估,看指标是否有提升;有提升则生长,否则提前停止生长
- 后剪枝:先长成一个大树,再试着把其中一些枝减掉,评估指标是否有提升,从而决定要不要剪
- 预剪枝训练时间短,存在欠拟合的风险
- 后剪枝训练时间长,能避免过拟合,泛化能力更强【更优】
- 工业界做法:直接限制树生长的深度
回归树
-
回归决策树的实质是对平面进行划分,划分后每个区域代表一个分支,取区域平均值作为预估值
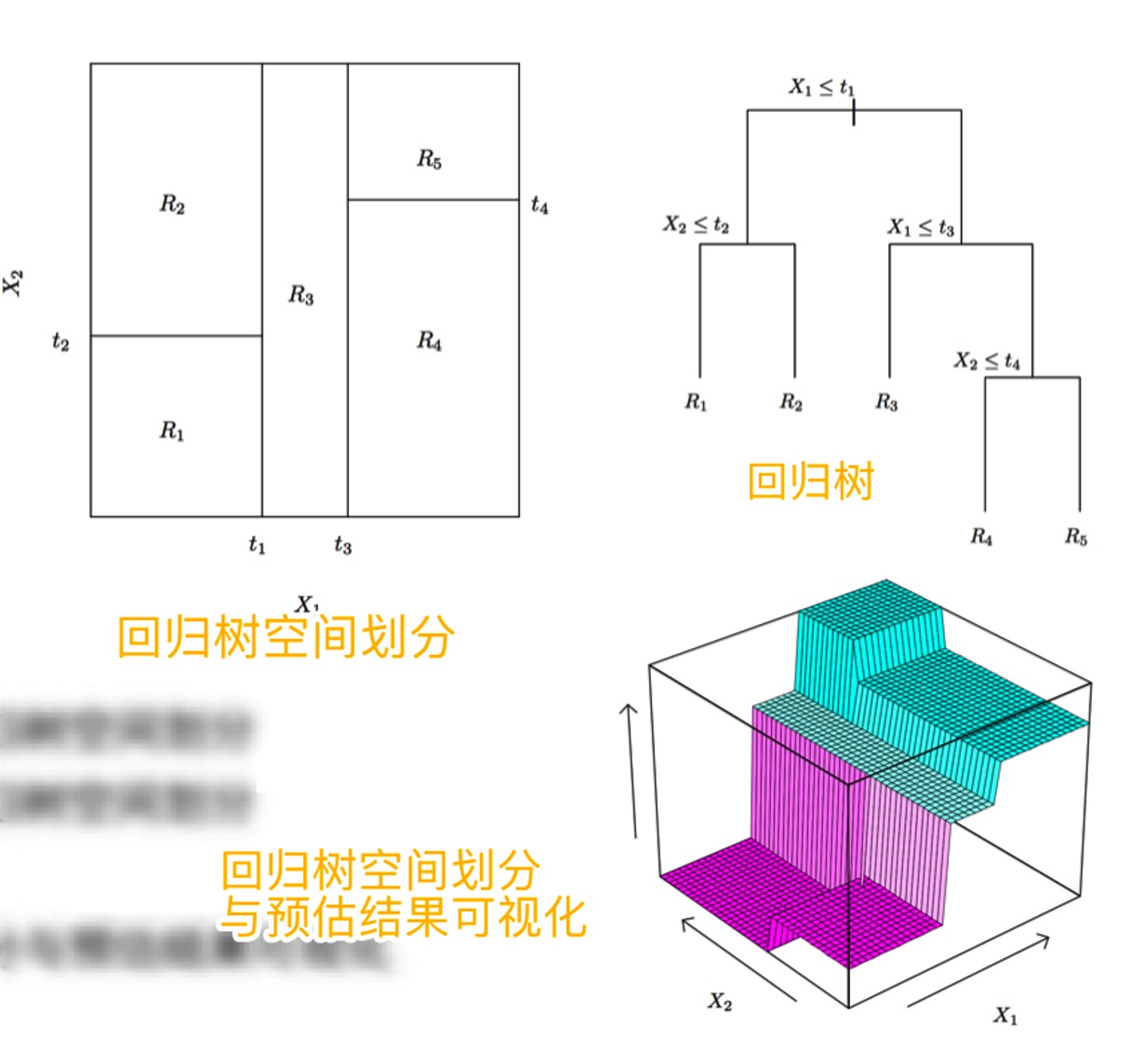
- 学习目标:遍历每个区域中, 每个样本与预测值(region平均)的误差平方和最小化 \(\sum_{j=1}^{J} \sum_{i \in R_{j}}\left(y_{i}-\widehat{y}_{R_{j}}\right)^{2}\)
- 算法:递归二分法
- Top-down:自上而下,把样本划分到两个区域
- Greedy: 每次划分只考虑当前最优
- Recursive: 选择合适的切分特征和切分点,不断划分使得RSS最小化
- 防止Overfitting的方法
- 正则化:对叶子节点个数进行惩罚,损失函数 + 正则化项 \(\sum_{m=1}^{|T|} \sum_{i \in R_{m}}\left(y_{i}-\widehat{y}_{R_{j}}\right)^{2}+\alpha|T|\)