假设检验与AB Test

100-Same Tree | Links:

I.假设检验的重要性

• 我们做实验的时候，通常接触不到population这个总体，因此我们通过样本来推测总体 ->这种inference就是假设
• 假设检验就是一种检验这种假设是否成立的方法

II.AB test

• 当产品测试一个新功能的时候，使用随机抽样对用户分成控制组和实验组。
• 控制组用户使用老版本，实验组用户使用新版本。来验证新功能是否能提升产品表现
• AB test原理基础是假设检验
• AB test在互联网产品中流行的原因
  • 软件产品更新迭代成本低
  • 数据量足够大

III.假设检验【AB Test】步骤

1.定义原假设 Null/备择假设 Alternative

• 原假设H0：无效，无差异（通常有等号=,≥,≤）
• 备择假设H1：有效，有差异
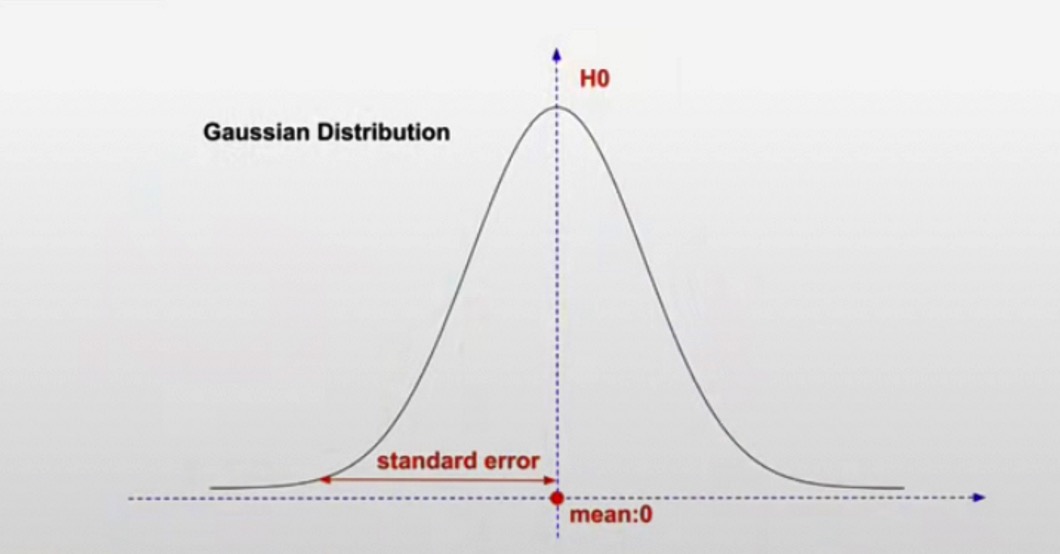
• AB test H0：新功能没有价值，mean(实验组)-mean(控制组)差值为0，H0描述了一个均值为0的正态分布
• AB test H1：新功能有价值，mean(实验组)-mean(控制组) 差值不为0，H1描述了一个均值不为0的正态分布
  
  
  

2.选择显著性水平significance level α

• 通常选择95%置信水平，α值为0.05
• 本质上是允许type I error出现的概率
  
  

3.确定检验功效和样本数量

• 检验功效【也是sensitivity】为1-β， 通常取值0.8
• β本质上是允许type II error出现的概率
• 根据α， power， based metric, 预期最小差异值可计算所需样本数量
  
  

4.计算检验统计量与检验p-value

• Z检验：已知标准差，检验两组均值
• T检验：不只标准差，检验两组均值
• Anova检验：检验三组以上均值
• Chi-sqaure卡方检验：检验分类数据之间的依赖关系
• p-value的实质：把H1假设测量的差值放到H0描述的正态分布里，计算在这个分布下这个差值出现的概率
  
  
  

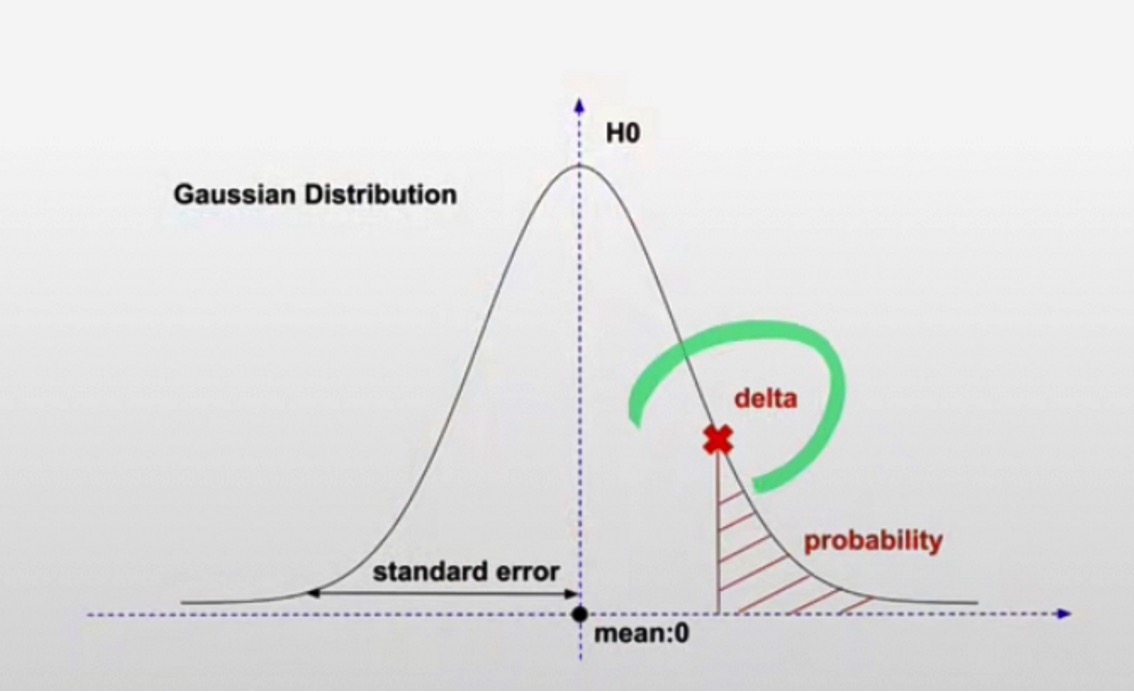
5.将检验p-value与显著性水平做比较，判断是否能否定原假设

• p-value <= 显著性水平：否定原假设，肯定备择假设
  • 等同说法：样本统计量与假设值之间具有统计意义上显著差异，不是偶然事件
  • p-value足够小说明这个H1描述的差值并不是由H0这个分布产生的， 可以推翻H0，认为新功能有价值
• p-value > 显著性水平,无法否定原假设，证据不足

IV.假设检验的两种错误

• 假设检验基于概率，因此始终存在出现错误的概率
• 两种错误的风险逆相关，并由显著性水平和检验功效来确定
  
  
  

Type I error: False positive

• 原假设为真，但遭到了否定，犯错概率为α。当否定原假设的时候，就要面对5%的犯错概率。
• 为了降低风险，要使用较低的alpha值
  
  

Type II error: False Negative

• 原假设为假，但无法否定它， 犯错概率为β，依赖于检验功效
• 为了降低风险，确保足够大的检验功效
  

V.AB test的几个预先假设与问题

• 样本大小：有足够大的样本来检测到差异
  • -> 需要计算样本大小和实验时间
• 随机化Randomization：实验组和控制组除了要测试的功能，其它是一模一样的。
  • -> 需要保证两组在所有特征上分布保持一致。
• 独立性Independency: 事件的发生是独立的，一个用户的行为不会另一个用户的行为产生影响。
  • -> 需要排除network effect
• 结果可泛化 Test results generalization: 实验结果可以泛化到所有用户在更长一段时间的表现。
  • -> 需要排除Novelty effect / Change Aversion

VI.样本大小问题

• 样本大小由预期最小变化幅度(metric baseline + improvement)，显著性水平α，功效1-β共同决定
• 显著性水平越小，功效越大，变化幅度越小 -> 需要的样本量越大
• 实际操作中，显著性水平（0.05）和功效（0.8）有常规取值，样本量的大小取决于预期最小变化幅度
  
  α vs. β trade-off
  
  
  
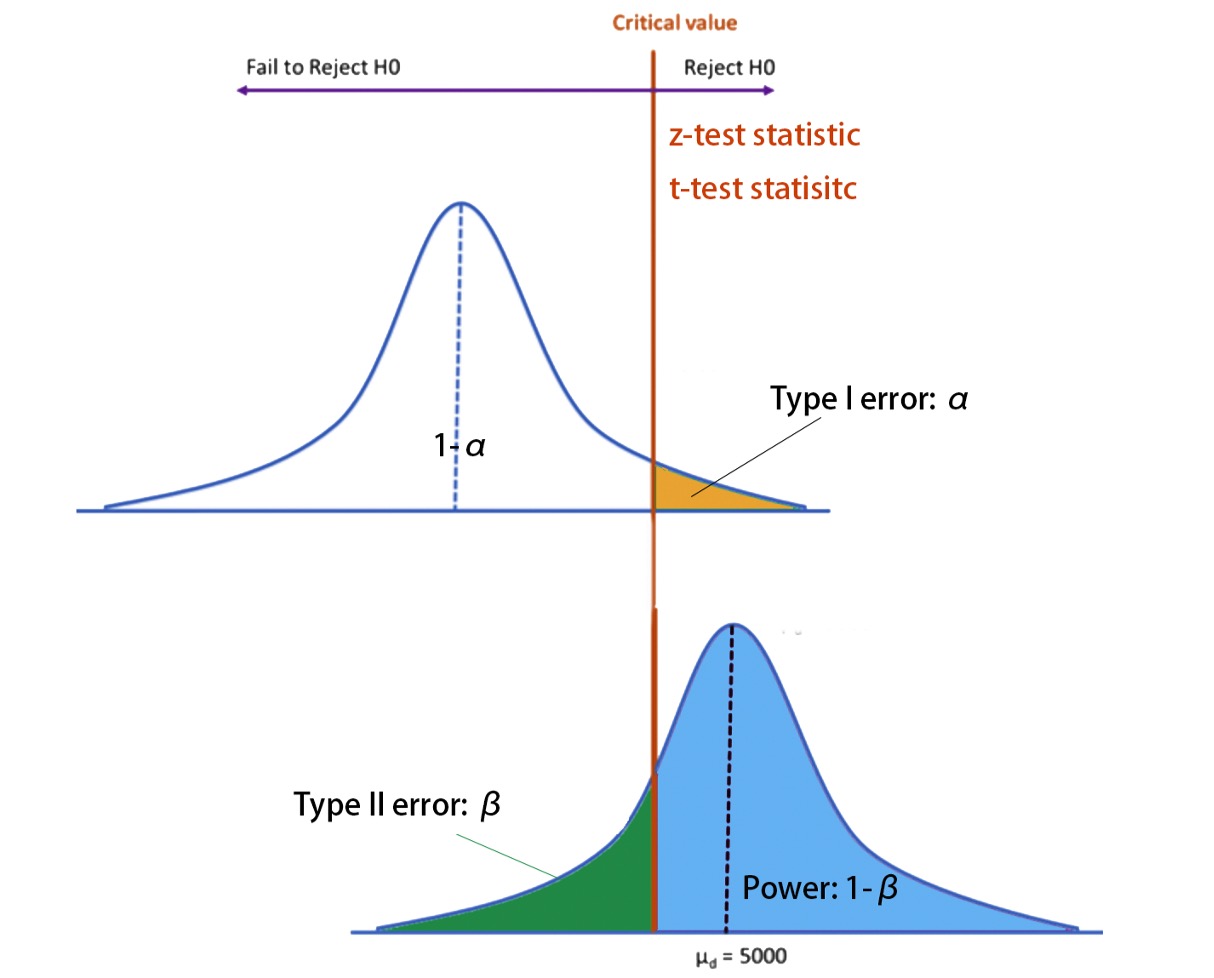
• α是允许type Error I出现的概率，β是允许type Error II 出现的概率
• 当α值设置很小，t检验值就会向右移动，β会变大
• 当样本量一定的情况下， α减小，β增大；α增大，β减小
• 要同时减小α，β，需要增大样本量
  
  计算所需样本大小的三种方法
• Built-in library
• Look up answer in a table
• Online calculator
  
  
  

import statsmodels.stats.api as sms
# Define the two conversion rates via proportion_effectsize. 
p1_and_p2 = sms.proportion_effectsize(0.10, 0.11)

# Calculate sample size
sample_size = sms.NormalIndPower().solve_power(p1_and_p2, power=0.8, alpha=0.05)
print("The required sample size per group is ~", round(sample_size))

确定实验时间

• 已知样本大小，根据每日流量可以计算实验所需时长 - 将流量对半分，分别进入实验组和控制组 - 取到足够的样本为止
• 基本经验 - 实验最少执行两周，以抓住weekly pattern，不足两周的补足两周时间 - 如果traffic很大，可以减小取样比例，通常互联网公司在小于1%的用户上进行实验

VII.统计意义上的显著性与实际显著性

• 统计意义的显著性并不意味着实际差值显著
• 样本量足够多或重复多次实验的时候，会提升小概率事件发生的概率，极小的差值会变得显著
• 考虑使用Bonferroni correction: α / number of tests

VIII.Randomization问题

• 控制组和实验组中的用户构成需要保持一致
• 验证方法
  • 单个特征验证：查看两组在某个特征上的分布
  • 自动化验证：机器学习树模型 + tree plot
    • 针对是否属于实验组建立tree model
    • 通过tree plot找分裂点
    • 如果控制组/实验组分布一致，则找不到分裂点；否则，分裂点即是分布不均衡的特征

IX.Novelty Effect问题

• 在控制组/实验组基础之上再分别分出新用户和老用户，分别进行AB test
• 如果新功能在老用户实验组胜出，但在新用户实验组失败，则是novelty effect的表现
• 由于新增分组，使用bonfferoni corrction调整p-value阈值：使用0.05/2进行判断

X.Sample Code